13.1 Introduction to Partial Differential Equations

We have previously discussed a lot of linear algebra and complex analysis, and we have seen how these topics are useful in physics. In this section, we will introduce the topic of partial differential equations (PDEs), which are equations that involve functions of multiple variables and their partial derivatives. PDEs are ubiquitous in physics; almost every field of physics uses PDEs to describe physical phenomena. In electrostatics, we have Poisson's equation (in Gaussian units)

and in electrodynamics, we have Maxwell's equations

The wave equation

is used to describe wave propagation, and the Schrödinger wave equation

is used to describe quantum mechanical systems.

Table of Contents

• Table of Contents
• Separation of Variables
• Separation of Angular Variables
• Eigenvalues of L² in Abstract Space (Ladder Operators)
  • Restricting the Eigenvalues
• Eigenvalues of L² in Function Space (Spherical Harmonics)
  • Integer Values of m
• Appendix: L Only Depends on Angular Variables

Separation of Variables

The first step in solving a PDE is to find a way to reduce the problem to a simpler one. One common technique is to use the method of separation of variables, which involves assuming that the solution can be written as a product of functions, each depending on only one of the variables. We typically assume that the solution can be written as

where is a function of the spatial coordinates and is a function of time . If we let be the spatial differetial operator that acts on , then we can rewrite the PDE as

The temporal component is usually a first or second order derivative, so most of our PDEs will look like

So we have, after separating variables,

We can then divide both sides by to get

As the left-hand side depends only on the spatial coordinates and the right-hand side depends only on time, the only way this can be true is if both sides are equal to a constant, which we will denote by ;

Notice that the time-dependent part of the equation is a first or second order ODE. The spatial part reduces to a PDE of the form

Generally, our expression for looks like

where is some function of the spatial coordinates, so

And rewriting (i.e., the spatial part of the solution), we have

We have a homogeneous PDE, which we typically solve using further separation of variables. The rest of these sections will be devoted to separation of variables in different coordinate systems.

Separation of Angular Variables

Define the momentum operator , and its th component is given by . This is the momentum operator in quantum mechanics if we multiply by . The commutation relations for the momentum operator are given by

The angular momentum operator is defined as , and its components are given by (with Einstein summation convention)

The commutation relations for the angular momentum operator are given by

The reason we are interested in the angular momentum operator is that it is dependent only on the agular variables and , and not on the radial variable . Moreover, as it is constructed from the momentum operator, its square is related to the Laplacian operator . Anyways, let's dot the angular momentum operator with itself to see what we get:

To proceed, we need to symmetrize the terms (so that we can collapse them back into a dot product). Therefore we use the commutation relations to write

which simplifies to

Finally, substituting back , we have

Rearranging this expression, and noting that , we get

So we have two important results here; first is a coordinate-independent expression for the Laplacian operator in terms of the angular momentum operator, and second is the expression for the Laplacian operator in spherical coordinates:

Going back to our homogeneous PDE , assuming that only depends on , we can substitute in the expression for the Laplacian in spherical coordinates to get

Let's now perform further separation of variables by assuming that , where is the radial part of the solution and is the angular part of the solution. Then substituting this into the PDE gives

Assuming, once again, that only acts on the angular part , we have after multiplying through by ,

(See the appendix for a justification of this step.) Letting the first term be and the rest be equal to , we have two separate equations:

The second equation is an ODE for the radial part , while the first equation is an eigenvalue equation for the angular part . We shall focus on the angular equation first. To do so, we need to find the eigenvalues and eigenfunctions of the operator .

Eigenvalues of L² in Abstract Space (Ladder Operators)

Let's consider an abstract vector space where a ket represents the angular part of the solution . The equation above is

Since is a derivative operator, it does not have a finite dimensional matrix representation, so we cannot find its eigenvalues by computing the characteristic polynomial.

Recall that a degenerate eigenvalue is one that corresponds to multiple linearly independent eigenvectors. In order to distinguish between these eigenvectors, we need to find another operator that commutes with so that we can simultaneously diagonalize both operators. A natural choice is another component of the angular momentum operator, . This is due to Theorem 6.4.18, which states that two normal operators are simultaneously diagonalizable if and only if they commute, as well as the fact that and are both Hermitian (self-adjoint) operators.

Anyways we have

where is the eigenvalue corresponding to .

In order to find the possible values of and , we can define the ladder operators. These are used in quantum mechanics to raise and lower the eigenvalues of angular momentum operators. For instance, a spin-1/2 particle has two possible spin states, spin-up and spin-down. The ladder operators can be used to transition between these two states. These are defined as

and they are Hermitian conjugates of each other, i.e., and . The commutation relations for the ladder operators are given by

Since commutes with either ladder operator, applying either ladder operator to an eigenvector of will yield another eigenvector with the same eigenvalue:

To verify that ladder operators do indeed raise and lower the eigenvalues of , we can compute

and similarly,

Combining these results, we see that

with being some constant that depends on the normalization of the eigenvectors. (In the context of group theory, the operator is known as a Casimir operator, which is an operator that commutes with all the generators of a Lie algebra. We will explore this topic further in later sections.)

Restricting the Eigenvalues

To find the possible values of and , we need to use the properties of the angular momentum operators. In every system like this, there exist maximum and minimum eigenvalues for ; in a spin-1/2 system with matrices, the maximum eigenvalue is and the minimum eigenvalue is . We shall try to find these maximum and minimum eigenvalues for the angular momentum operators.

First, we note that is a positive semi-definite operator, since it is the sum of squares of Hermitian operators. A positive operator is characterized by for all vectors in the vector space. Therefore, we have

so .

Next, we can express in terms of the ladder operators. To do so we first compute

and similarly,

Adding these two expressions together gives

Therefore we have

which simplifies to

Since , we have

As the norm term is non-negative, we have

We can add these two inequalities together to get

So this places a restriction on the possible values of given a value of . Let the highest eigenvalue of be and the lowest eigenvalue be . Then applying the ladder operators to these eigenvectors must give zero, otherwise we would be able to raise or lower the eigenvalues indefinitely, which contradicts our assumption that and are the maximum and minimum eigenvalues, respectively. Therefore we have

Plugging in into the earlier expression for , we have

and plugging in gives

Solving these two equations simultaneously gives

We must have , so we take the positive sign for and the negative sign for , giving

The takeaway is this: if we have any eigenvector , we can apply the ladder operators to reach the maximum and minimum eigenvectors. Therefore, there must be some integer such that repeated application of the lowering operator on the highest eigenvector gives the minimum eigenvector:

This means that is the minimum eigenvector, so

Since , we have

Substituting this back into the expression for , we have

These results can be stated in theorem form.

Theorem 13.3.1 (Eigenvalues of L² and Lz)

The eigenvalues of the operator , denoted , are given by the relations

where is a non-negative integer or half-integer (i.e., ) and takes values in the set .

We also need to address the normalization of the eigenvectors. We know that the eigenvalues of are orthogonal, since is a Hermitian operator. By convention, we will normalize the eigenvectors such that

Let's find the norm of the laddered eigenvectors. We have

Thus,

Substituting in the earlier expression for in terms of the ladder operators, then using the theorem, we obtain

We drop the phase factor by choosing to be real.

Box 13.3.2 (Ladder Operator Action on Eigenvectors)

The action of the ladder operators on the eigenvectors is given by

Example 13.3.3 (Positive Integer j)

Let be a positive integer. Then the possible values of are , giving a total of eigenvectors for each value of .

We can find a closed-form expression for the eigenvectors by starting from the highest eigenvector and applying the lowering operator repeatedly. We have

Eigenvalues of L² in Function Space (Spherical Harmonics)

Now we can return to the original problem of finding the angular part of the solution by solving the eigenvalue equation

Let's consider each component of the angular momentum operator in spherical coordinates. The eigenvalue equation for is given by

Let's separate variables by assuming that . Substituting this into the eigenvalue equation and dividing through by gives

This is an ODE for , and its solution is

where is a constant, which we can absorb into the normalization of later. Anyways we now have

Integer Values of m

We will first consider the case where is an integer. This is to make the solution single-valued, since is periodic with period , as classical physics requires. In quantum mechanics, however, half-integer values of are also allowed, which leads to the concept of spin. To distinguish between these two cases, we will denote the integer case with , where is a non-negative integer.

We will need to find expressions for the ladder operators in spherical coordinates. Using the earlier expressions for and , we have

Recall that is the maximum eigenvalue of . Therefore, applying the raising operator to must give zero:

This simplifies to

which is an ODE for with solution

So the highest eigenfunction is

To find the rest of the eigenfunctions, we simply apply the lowering operator repeatedly. Using the earlier expression for , we have

It can be shown that applying the term in parentheses gives

So using that and , we have

Repeatedly applying the lowering operator will lead to the general expression

where we have made the substitution . Letting , we have (using Example 13.3.3)

Finally, we can determine the normalization constant by taking (since the constant is independent of ) and obtaining

This is just the Legendre polynomial multiplied by a constant;

so we can use the normalization condition for Legendre polynomials to find . Using

(the completeness relation for spherical coordinates), we have

Substituting gives

It can be shown that this leads to

Thus, the final expression for the eigenfunctions is

with . This set of functions are known as the spherical harmonics. They appear frequently in physics, anywhere the Laplacian is expressed in systems with spherical symmetry. The atomic orbitals of electrons in atoms are described by spherical harmonics, for example.

The part is

but for historical reasons, we use the associated Legendre functions defined by

We thus have

Box 13.3.4 (Spherical Harmonics)

The spherical harmonics, which are solutions to the angular part of the Laplace equation in spherical coordinates, are given by

where is a non-negative integer, takes values in the set , and are the associated Legendre functions defined by

Visualization of spherical harmonics for to and to . The color indicates the phase of the function, while the radius indicates the magnitude. (Source: Wikimedia Commons)

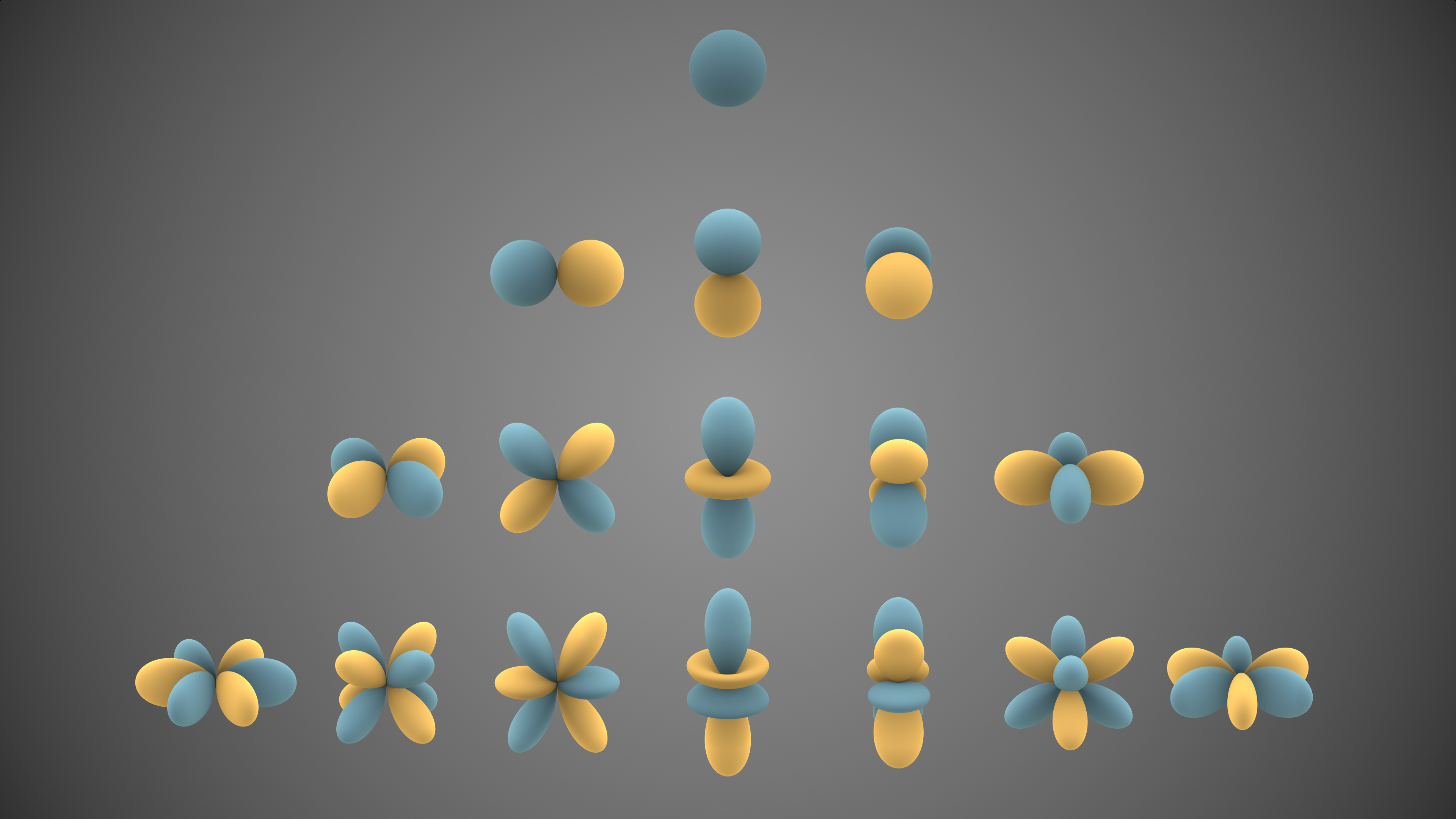
Appendix: L Only Depends on Angular Variables

To justify the step where we assumed that only acts on the angular part , we can express in spherical coordinates.

Let be the th component of the angular momentum operator. Acting on a function , we have

Let's convert this to spherical coordinates using the respective transformations

Using the chain rule, we have

Calculating the partial derivatives (using the transformations above), we have

Now we can use these expressions to rewrite in spherical coordinates. First, for we have

so

Similarly, for we have

so

Finally, for we have

so

Now we can compute . For we have

Similarly, for we have

And for we have

Adding these three expressions together, we have

In the last step we used a reverse product rule to rewrite the first two terms. This final expression for only involves derivatives with respect to the angular variables and , confirming our earlier assumption.